TensorFlow
in AI with 0 comment
TensorFlow

TensorFlow

in AI with 0 comment

TensorFlow

1 TensorFlow

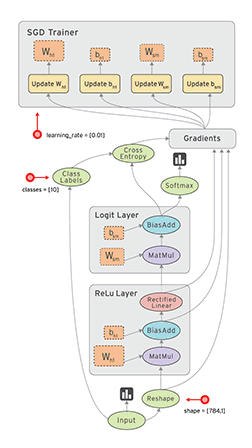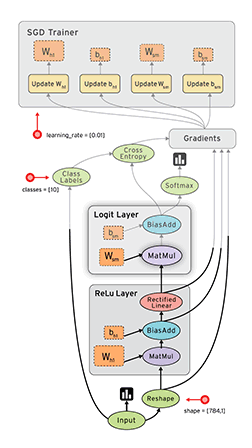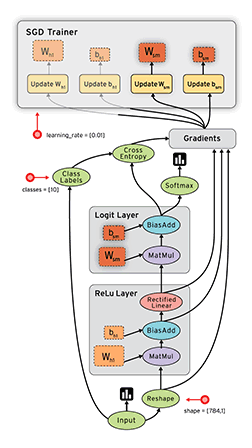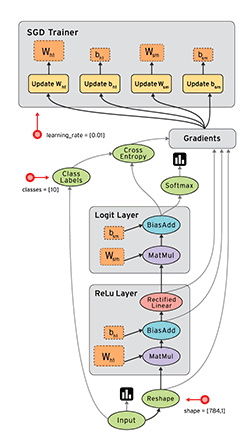
在这里插入图片描述

TensorFlow™ 是一个采用数据流图（data flow graphs），用于数值计算的开源软件库。
节点（Nodes）在图中表示数学操作，图中的线（edges）则表示在节点间相互联系的多维数据数组，即张量（tensor）。
它灵活的架构让你可以在多种平台上展开计算，例如台式计算机中的一个或多个CPU（或GPU），服务器，移动设备等等。TensorFlow 最初由Google大脑小组（隶属于Google机器智能研究机构）的研究员和工程师们开发出来，用于机器学习和深度神经网络方面的研究，但这个系统的通用性使其也可广泛用于其他计算领域。

1.1 为什么要使用tensorflow

支持GPU,TPU加速
实现自动求导
有丰富的神经网络API
成为TFBOYS 0

1.2 TensorFlow的安装

目前使用的版本为TensorFlow-2.2.0,由于1.x与2.x很多api不兼容,所以如果学习过1.x,请忘记他.

1.2.1 进入conda环境

在这里插入图片描述

在这里插入图片描述

1.2.2 更新pip

python -m pip install --upgrade pip

1.2.3 安装tensorflow

pip install tensorflow-cpu==2.2.0 -i https://pypi.douban.com/simple

1.2.4 测试

  1. 进入python命令行
python

在这里插入图片描述

  1. 导包并打印版本
import tensorflow as tf
tf.__version__

在这里插入图片描述

如果导包失败报错如下

>>> import tensorflow
Traceback (most recent call last):
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\python\pywrap_tensorflow.py", line 58, in <module>
    from tensorflow.python.pywrap_tensorflow_internal import *
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\python\pywrap_tensorflow_internal.py", line 28, in <module>
    _pywrap_tensorflow_internal = swig_import_helper()
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\python\pywrap_tensorflow_internal.py", line 24, in swig_import_helper
    _mod = imp.load_module('_pywrap_tensorflow_internal', fp, pathname, description)
  File "D:\utils\Anaconda\lib\imp.py", line 242, in load_module
    return load_dynamic(name, filename, file)
  File "D:\utils\Anaconda\lib\imp.py", line 342, in load_dynamic
    return _load(spec)
ImportError: DLL load failed: 找不到指定的模块。

During handling of the above exception, another exception occurred:

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\__init__.py", line 41, in <module>
    from tensorflow.python.tools import module_util as _module_util
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\python\__init__.py", line 50, in <module>
    from tensorflow.python import pywrap_tensorflow
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\python\pywrap_tensorflow.py", line 69, in <module>
    raise ImportError(msg)
ImportError: Traceback (most recent call last):
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\python\pywrap_tensorflow.py", line 58, in <module>
    from tensorflow.python.pywrap_tensorflow_internal import *
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\python\pywrap_tensorflow_internal.py", line 28, in <module>
    _pywrap_tensorflow_internal = swig_import_helper()
  File "D:\utils\Anaconda\lib\site-packages\tensorflow\python\pywrap_tensorflow_internal.py", line 24, in swig_import_helper
    _mod = imp.load_module('_pywrap_tensorflow_internal', fp, pathname, description)
  File "D:\utils\Anaconda\lib\imp.py", line 242, in load_module
    return load_dynamic(name, filename, file)
  File "D:\utils\Anaconda\lib\imp.py", line 342, in load_dynamic
    return _load(spec)
ImportError: DLL load failed: 找不到指定的模块。


Failed to load the native TensorFlow runtime.

See https://www.tensorflow.org/install/errors

for some common reasons and solutions.  Include the entire stack trace
above this error message when asking for help.

说明缺少环境,请访问
https://support.microsoft.com/zh-cn/help/2977003/the-latest-supported-visual-c-downloads
下载对应的 vc_redist.x64.exe 进行安装

在这里插入图片描述

1.2 回归问题

1.2.1 函数图像绘制

https://www.desmos.com/calculator

Linear Equation线性方程
y = a * x + b
1.6 = a * 1 + b
3.1 = a * 2 + b
由上解出 a = 1.5 b = 0.1

但是这样的方程在现实生活中往往很难遇到。
以下的方程才是常见的情况，他们一般都有包含噪声（with noise）
y = w * x + b + ε
ε (Epsilon)为噪声值
ε ~ N(0,1) 正态分部
当函数存在噪声时，我们需要观察多组数据才能近似确定w、b的值
如何解决这个问题呢？

1.2.2 损失函数

基于上边的例子，我们可以得到下边的一个损失函数
Loss = Σi(a * xi + b -yi) ²/n
也就是均方差MSE

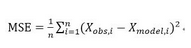
在这里插入图片描述

求得loss的最小值方法为对loss进行梯度下降计算，当loss值为最小时，即得
a’ b’的最佳值。
然后针对loss求极小值（Minisize loss）
最终得到f(x) = a’ * x + b’ 中a’和b’

1.2.3 梯度下降

如果将loss函数以图像的方式来表示的话,如下图:自变量有a和b,应变量为f(x)

在这里插入图片描述

图中每个点都可以在一个三维坐标系中来表示,如下:
我们可以通过计算某个点所处的切面方向来推导出该点向哪个方向移动即可找到f(x)更小的值,重复计算并移动该点则可以在整个取值范围内找到函数图像的最低点,也就是loss函数的最小值.

在这里插入图片描述

为了方便理解,我们把三维模型转换为二维来进行讲解,随着由两个自变量变为一个自变量,在降维的同时我们开始提到的计算某个点的切面变成了计算某个点的切线(也就是导数).

在这里插入图片描述

通过观察发现.导数为正数时,函数图像处于上升阶段,所以极小值应该在左边,所以自变量应该调小,而当导数为负数时,函数图像处于下降阶段,自变量相应调大,至于调整多少一般情况下我们会直接引用导数进行计算.考虑到在导数绝对值较大情况下,自变量变化的步长就会较大,所以通常会在导数上乘以一个较小的数来缩短步长.
如: a b = a b − f ′ ( a b ) ∗ 0.001 ab = ab - f’(ab) * 0.001ab=ab−f′(ab)∗0.001
经过多次计算之后,自变量会在极小值左右反复来回移动,直到停滞在最小值上.

有的时候也会存在如上图一样在一定范围内有多个凹陷的部分,为了防止开始计算时的选点不在有最小值的凹陷内,我们通常会进行随机选多点的方式进行同步计算,找到最小值.

1.2.3 TF实现线性回归案例

以下数据为受教育年限与平均收入的对应表,根据数据样本展示的特点进行训练建模,并以此预测小,初,中,本,研的薪资水平(数据来源为网络,只做知识练习层面讨论.)

ID,Education,Income
1,10.000000 ,26.658839
2,10.401338 ,27.306435
3,10.842809 ,22.132410
4,11.244147 ,21.169841
5,11.645449 ,15.192634
6,12.086957 ,26.398951
7,12.048829 ,17.435307
8,12.889632 ,25.507885
9,13.290970 ,36.884595
10,13.732441 ,39.666109
11,14.133779 ,34.396281
12,14.635117 ,41.497994
13,14.978589 ,44.981575
14,15.377926 ,47.039595
15,15.779264 ,48.252578
16,16.220736 ,57.034251
17,16.622074 ,51.490919
18,17.023411 ,51.336621
19,17.464883 ,57.681998
20,17.866221 ,68.553714
21,18.267559 ,64.310925
22,18.709030 ,68.959009
23,19.110368 ,74.614639
24,19.511706 ,71.867195
25,19.913043 ,76.098135
26,20.354515 ,75.775216
27,20.755853 ,72.486055
28,21.167191 ,77.355021
29,21.598662 ,72.118790
30,22.000000 ,80.260571
12345678910111213141516171819202122232425262728293031

首先通过数据进行图像绘制

import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt

# 通过pd读取文件
data = pd.read_csv('./data.csv')
x = data.Education
y = data.Income
# 通过plt绘制图像
plt.scatter(x, y)
plt.show()
1234567891011

在这里插入图片描述

通过对上图的观察.我们可以发现整体数据体现出哪些特征?

  1. 受教育年限与收入正相关
  2. 在二维空间中,两者之间呈现比较明显的线性关系
    那么我们就可以来使用
    f(x) = ax + b
    来尝试进行模型的建立.
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt

# 通过pd读取文件
data = pd.read_csv('./data.csv')
x = data.Education
y = data.Income
# 通过plt绘制图像
plt.scatter(x, y)
# plt.show()

# 顺序模型&序贯模型初始化
model = tf.keras.Sequential()
# 传入Dense层,指定输出维度为1 输入维度为1
model.add(tf.keras.layers.Dense(1, input_shape=(1,)))
# 展示模型
# model.summary()

# 创建模型,指定优化器和损失函数
model.compile(optimizer='adam', loss='mse')
# 保留训练过程,指定训练数据和训练次数,并得到最终模型.此时model已经保存了训练完毕的模型.
history = model.fit(x, y, epochs=50000)

# # 使用训练完毕的模型预测数据得到预测结果
x1 = x
y1 = model.predict(x)

# 讲预测结果绘制为图像用于对比原数据,评估契合度
plt.scatter(x1, y1)
plt.show()

# 预测在受教育年限为6,9,12,16,20年时,薪资水平分别是多少
fx = model.predict([6, 9, 12, 16, 20])
print(fx)

1.3 基础API

基础数据类型
Tf.constant,tf.string
Tf.ragged.constant,tf.SparseTensor,tf.Variable
自定义损失函数—tf.reduce_mean
自定义层次—Keras.layers.Lambda和继承法
Tf.function
Tf.function,tf.autograph.to_code,get_concrete_function
graphDef
get_operations,get_opration_by_name
get_tensor_by_name,as_graph_def
自动求导
Tf.GradientTape
Optimzier.apply_gradients

HelloWorld
Google提供的tensorflow学习平台
https://developers.google.cn/machine-learning/crash-course
tensorflow测试平台
http://playground.tensorflow.org

归一化

回调函数

本文由 liyunfei 创作，采用 知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: Jun 24,2022